Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science, under discrete mathematics (a section of Mathematics and also of Computer Science). Automata comes from the Greek word αὐτόματα meaning "self-acting".
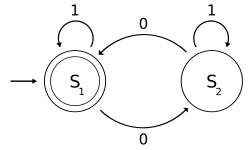
The figure at right illustrates a finite state machine, which belongs to one well-known variety of automaton. This automaton consists of states (represented in the figure by circles), and transitions (represented by arrows). As the automaton sees a symbol of input, it makes a transition (or jump) to another state, according to its transition function (which takes the current state and the recent symbol as its inputs).
Automata theory is also closely related to formal language theory. An automaton is a finite representation of a formal language that may be an infinite set. Automata are often classified by the class of formal languages they are able to recognize.
Automata play a major role in theory of computation, compiler design, artificial intelligence, parsing and formal verification.
Automata are defined to study useful machines under mathematical formalism. So, the definition of an automaton is open to variations according to the "real world machine", which we want to model using the automaton. People have studied many variations of automata. The most standard variant, which is described above, is called a deterministic finite automaton. The following are some popular variations in the definition of different components of automata.
https://en.wikipedia.org/wiki/Automata_theory
No comments:
Post a Comment